Shower Accoustics
Playing with Sound
Following a lecture today, it was suggested that us students sing in the shower and notice how the apparent intensity of the sound changes depending on the pitch. Of course, the goal of this was to find the resonant frequency of our shower. I thought this would be fun to quantify and it also gave me an idea for investigation:
Can we estimate the dimensions of a shower based off the resonant frequencies?
Naively, I went about exploring this.
Generating the Sweep
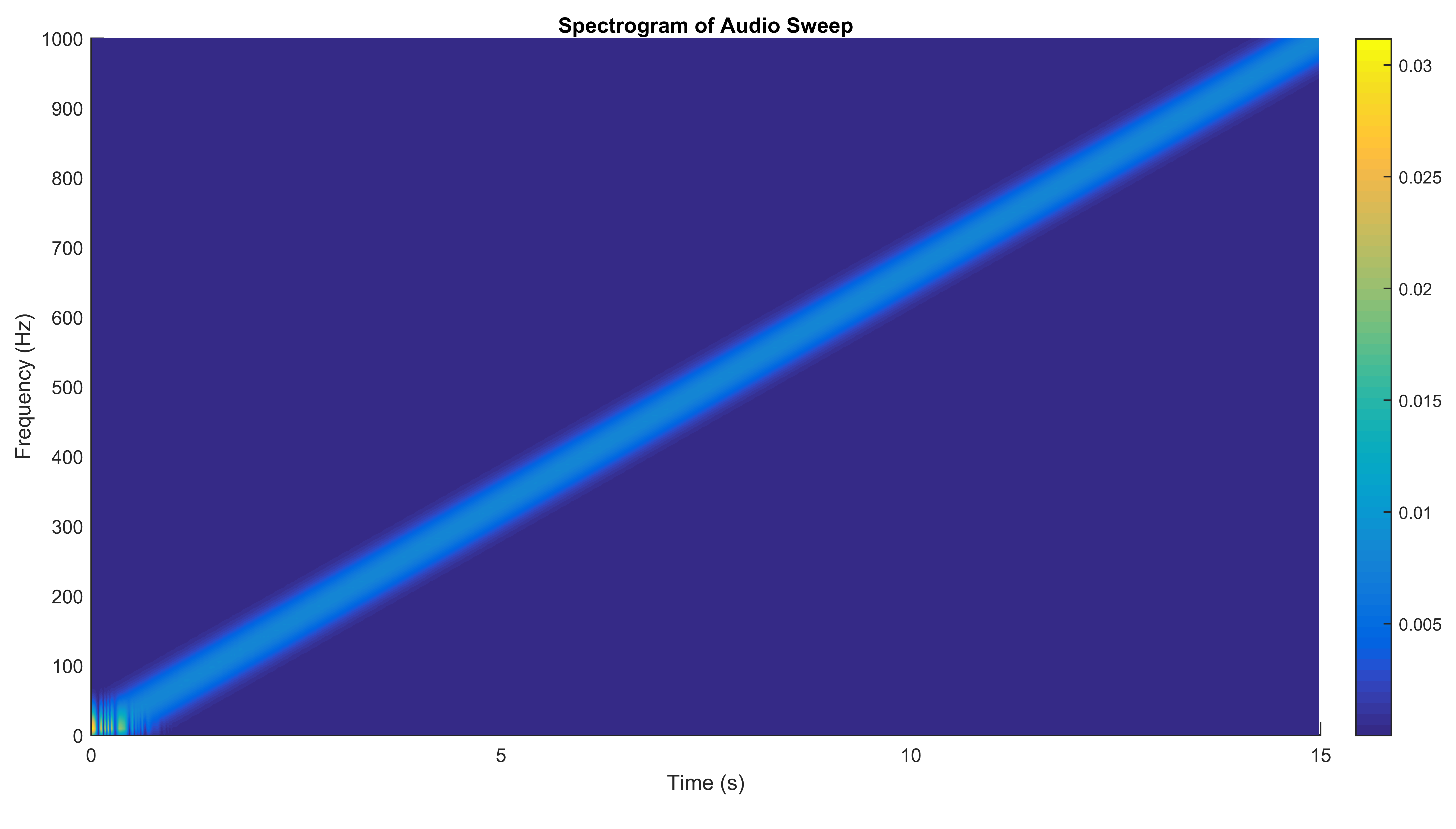
The first step was to create an audio file where all the frequencies are swept through in at a constant speed at a constant intensity. I did this in matlab. My version of matlab (2015a) has a built-in function called chirp that generates a swept-frequency cosine signal.
I decided to go through the frequenecy range [0, 1000] Hz, use the standard sampling rate of 44.1 kHz, and have the sweep take 15 seconds. The full command was:
tot=15; % sweep time (s)
fs=44100; % sampling frequency (hz)
t = 0:1/fs:tot;
y = chirp(t,0,tot,1000);
The output generated:
Converting this to a spectrogram, we see a nice uniform sweep
Playing the Sound
Athough some experiments are in need, I thought I would jump to the chase: I happened to have a small bluetooth speaker around, so I used that to generate the sound. I also measured the dimensions of my shower to be about 57 x 22 inch
Analyzing the Spectrum
Bringing the audio back into matlab and then looking at the spectrum, we see that the intensity is not uniform! A promising sign
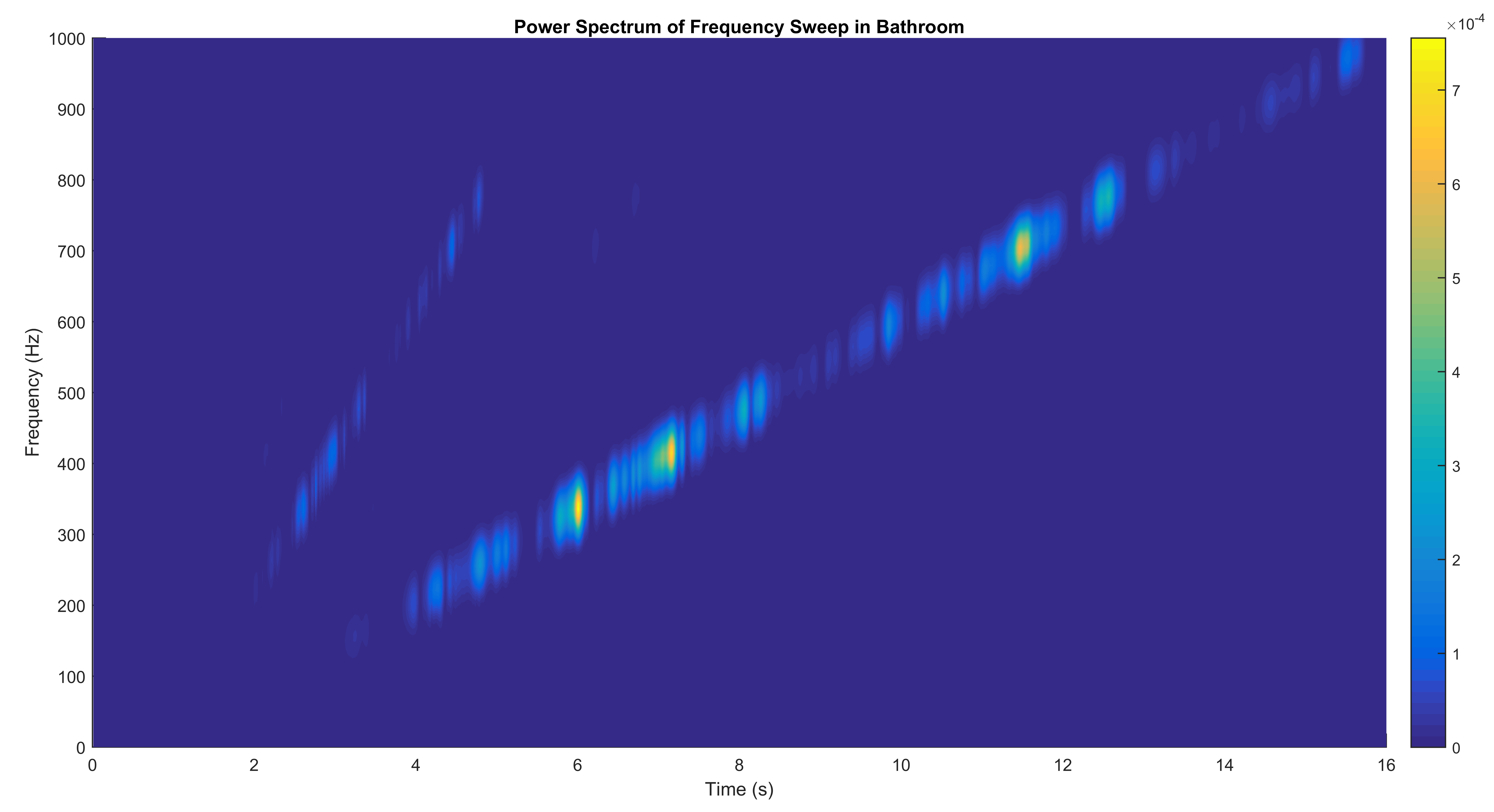
We can notice that there are two dominant frequencies that pop out, and then also their approximate harmonics!
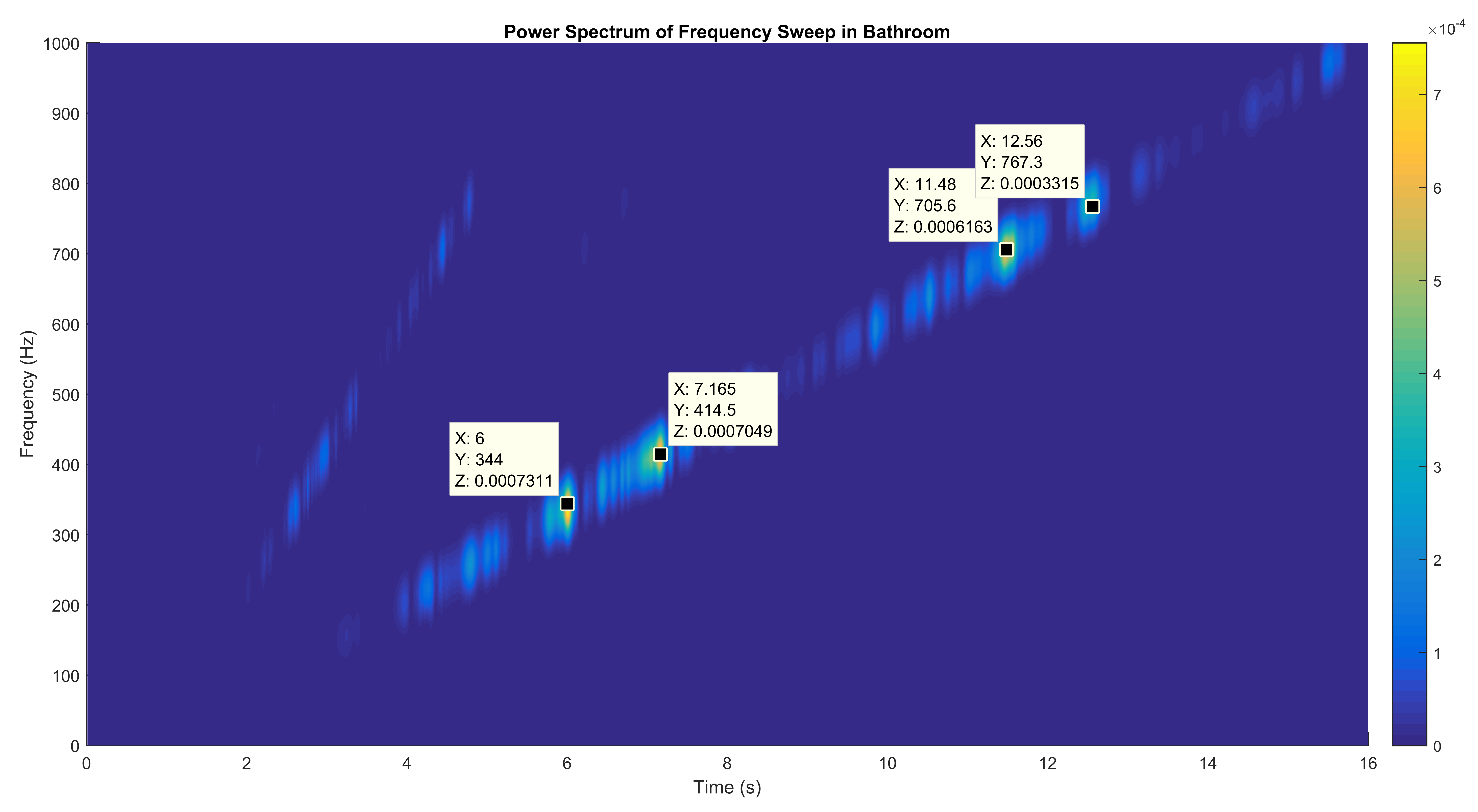
Two dominant frequencies that appear are 344 Hz and 414.5 Hz. We can now use this to estimate the shower dimensions.
Estimating Dimensions
Using an estimated speed of sound (using the barometric pressure and temperature), we can plug and chug:
\[c = 1123.32 \text{ ft/s}\] \[\lambda = \frac{c}{\omega}\] \[\lambda \approx .0402 \text{ in}\]We can see that the resonant frequency has a pretty small associated wavelength. We might hope that this frequency is a harmonic of the fundamental. In this case, since the shower has a rectangular shape, we might expect two harmonic frequencies: one that corresponds to the length, and one that corresponds to the width.
The powers that approximetaly put us in this range are 2^9 and 2^11 (respectivly).
ss = 1123.32; % Speed of Sound
freq = 344.2;
(ss*12) / ((freq/(2^9))*1000)
freq = 414.5;
(ss*12) / ((freq/(2^11))*1000)
Generates:
20.0514
66.6024
Maybe??
I will point out, I think that is actually unlikely to be what we think it is. It seems likely to me that the result might actually reflect something about the microphone in my phone or the bluetooth speaker. Either way, it was cool none the less to see that our frequency response to the sweep was far from flat!
Validating Approach
In order to see if the results are sensible, I thought two experiments would be:
- Placing speaker in a box of known dimension to estimate any correction factors
- Play outside in open area to see how flat the frequency response is when no resonant frequencies are expected
These tasks are ongoing projects!