L1 Norm
A somewhat common question that often gets asked in linear regression is: Why do we minimize the square of the residuals? It might seem more natural to simply minimize the absolute value of the residuals.
I remember that when I asked this question some people commented on the fact that the derivative exists for \(f(x)=x^2\) but not for \(f(x)=\|x\|\). This makes it easier to prove that there is a unique analytic solution, but surely in the age of computers this isn’t an issue. It turns out this explaination is just a part of the story.
The question of why square the errors has been addressed in several posts online 1 2, so I do not intend for this to be original, just my own stab at summarizing the explaination.
We will consider the simplest case of univariate linear regression. In this case: \(c=\lambda\)
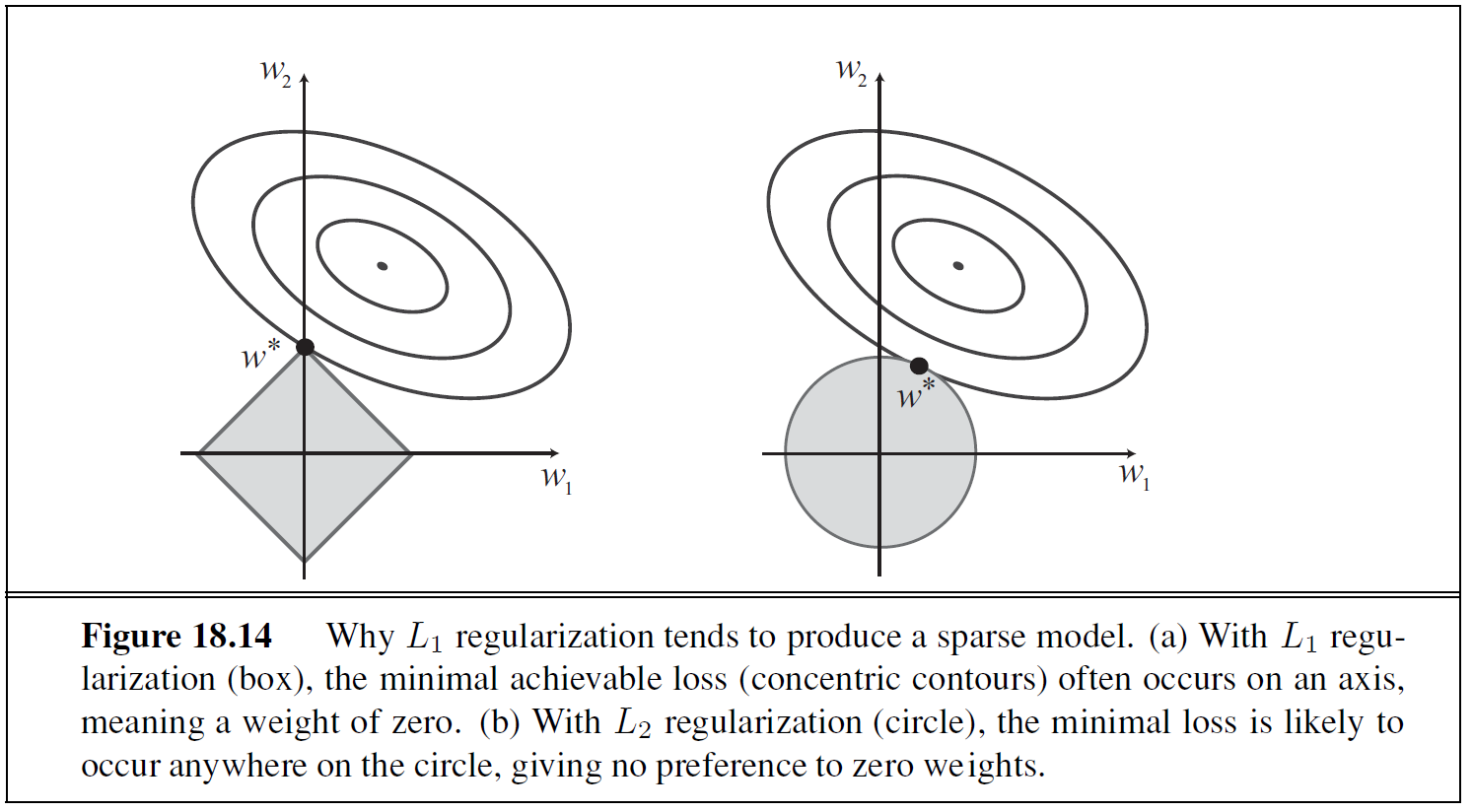
\[\hat{y}= f_w(\textbf{x})=w_n x_n\]To find the best estimates of w, we can use the L2 norm of the loss function, for which we get a new function of \(w\), namely, \(Loss(h_\textbf{w}\) This has a unique standard solution which can be found in the usual way. For linear functions, this is always convex. In practice, we might be concerned with overfiting, and thus need regularization. We thus update the cost function with a regularization term
\[Cost(f)= EmpLoss(f_w(x)) + \lambda Complexity(w)\]A general family of regularization functions is just the norm of the coefficients! This is where L1 regularization is beneficial. We can get a feel for this by considering a an upper limit for the complexity (\(Complexity(w) \leq c\)). This means that we are trying to minimize the cost within the regular unit circle of the norm. In general, L_2 minumums are equally likely to occur anywhere on the edge of the circle, but more likly to occur on the corner of the box!